Bayes’ Rule
The
Bayes’ rule was named after the famous English Statistician Thomas Bayes. Using the
Bayes’ rule, one can find the conditional probability of one occurring one event
given another if the prior knowledge of conditions is known.
Let
A and B be two events that occur one after another. Suppose you have already known the conditional probability of occurring an event B give A and one is interested in finding the conditional probability of occurring event A given B. Then it is given by the Bayes’
rule as follows.
Let
us understand the Bayes’ rule with the help of an example as follows.
Example
There are three factories responsible for producing certain components that are distributed to other companies to be used. All factories produce defective components that occur at random. Factory A is used 60% of the time, factory B 15% of the time, and C 25% of the time. Factory A produces components with a 15% defective rate, B at a rate of 10%, and C at 5%. You receive a shipment from one of the factories, and you examine one component after the other. It takes 18 components to find the first defective one.
- Without calculating, which factory do you think is most likely to have shipped this batch of components? Briefly explain how you decide this.
- Find the probability the shipment came from factory C. Round intermediate steps to four decimal places. Show your work, including variable definition and declaring their distributions.
Solution
Part A)
Factory
C is most likely to have shipped this batch of components.
Because factory C produces components with a 5% defective rate which is lower than
all the factories. Moreover, factory C is used 25% of the time while factory A is used 60% of the time and factory B is used 15% of the time.
Part B)
Given
There are three factories responsible for producing certain
components that are distributed to other companies to be used. All factories
produce defective components that occur at random. Factory A is used 60% of the
time, factory B 15% of the time, and C 25% of the time.
Let, P(A) denote the probability that factory A is used for the shipment.
P(B) denotes the probability that factory B is used for the shipment.
P(C) denotes the probability that factory C is used for the shipment.
This gives, P(A) = 0.60, P(B) = 0.15 and P(C) = 0.25.
Factory A produces components with a 15% defective rate, B at a
rate of 10%, and C at 5%. Let D be the event of defective components in the
shipment.
This gives, P(D | A) = 0.15, P(D | B) = 0.10, P(D | C) = 0.05.
To find
The
probability the shipment came from factory C given that the first defective
component was found at 18th selection.
Let
“E” be the event that among the first 18 components detected, the last component
(18th Component) is defective. The probability of interest is P(C |
E).
P(E
| A) = Probability of getting first defective component on 18th selection
in Factory A.
P(E
| B) = Probability of getting first defective component on 18th
selection in Factory B.
P(E
| C) = Probability of getting first defective component on 18th
selection in Factory C.
So
first find P(E | A), P(E | B), and P(E | C).
Identify the distribution in this case
Observe that, the trials have
binary outcomes, that is defective and non-defective components. Each trial is
independent of one another. The random variable counts the number of
non-defective components before the first defective components.
Therefore, we use geometric probability
distribution to find the probabilities P(E | A), P(E | B), and P(E | C).
P(E | A) = 0.15*(1-0.15)17 = 0.0095.
P(E | B) = 0.10*(1-0.10)17 = 0.0167.
P(E | C) = 0.05*(1-0.05)17 = 0.0209.
Law of total probability
P(E) = P(E | A)*P(A) + P(E | B)*P(B) + P(E
| C)*P(C).
Bayes’ rule
Using the law of total probability; P(E) = 0.0095*0.60 + 0.0167*0.15 +
0.0209*0.25 = 0.01343.
Using Bayes’ rule,


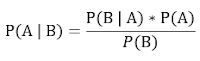


0 Comments
Post a Comment