Jacobian transformation method to find marginal PDF of (X+Y)
It
is always challenging to find the marginal probability density functions of
several random variables like √X, (1/X), X+Y, XY, etc. when we know the
marginal and/or joint probability density functions. We call these variables
like √X, (1/X), X+Y, XY, etc. as transformations. Jacobian transformation
method is one of the methods which is widely used to find marginal pdfs of such
transformations. Let us understand how to use the Jacobian transformation
method with the help of an example.
Question
Let
X and Y be independent, continuous random variables with probability density
functions (PDFs) as follows.

Use the Jacobian transformation method to calculate the PDF of X+Y.
Solution
We
have two continuous random variables X and Y with their PDFs as follows.
Step 1: Obtaining joint probability distribution for (X, Y)
Two
continuous random variables, X and Y, are independent if we can write the joint
PDF of (X, Y) as a product of their marginal PDFs. In this case, we know that
the random variables X and Y are independent. Therefore, the joint PDF of
(X, Y) is given as follows.
Step 2: Obtaining range for newly defined variables
We
need to find a marginal PDF of X+Y, for this, we define U=Y and V=X+Y.
We will use the Jacobin transformation method to obtain the joint pdf of U, V.
Then we try to define X and Y in terms of U and V as follows.
Recall the ranges of variables X and Y as, x ≥ 0, y ≥ 0. From these, we can easily obtain the ranges of random variables U and V as,
Step 3: Obtaining Jacobian (J)
The
Jacobin | J | can be defined as follows,
From this we get,
This gives,
Step 4: Obtaining joint probability distribution for (U, V)
Therefore,
we can obtain the joint pdf of (U, V) as follows.
This is the required joint PDF of (U, V). But we need to find the PDF of V=X+Y, for this, we proceed as follows.
Step 5: The marginal probability distribution of X+Y
Summarizing
this, we get the marginal PDF of V = X+Y as follows.







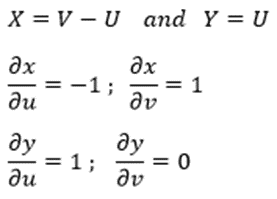




0 Comments
Post a Comment