Introduction
Many of you might have known what a normal distribution is. If you do not know, please refer to the blog on a normal distribution. Here you will get learn how to use the TI84 calculator to find normal probabilities or critical values.
TI83/TI84
calculator is a modern scientific calculator wherein various mathematical, as well as statistical calculations, are possible. One can use the calculator to
graph the functions but there are some limitations too. Let us not get into
more details and focus on how to calculate normal probabilities or
critical values using the TI84 calculator.
Use of TI84 calculator to find normal probabilities
In hypothesis testing, we use the normal distribution to test the claim about
population mean (µ) if we know population standard deviation (σ) in prior. In
this situation, we use standard normal distribution or Z distribution hence we
call it as Z test. While using the Z test we need to find the p-value for making
decisions. Finding a p-value is the same as finding normal probability for the given
test statistic. We can use the following procedure to find p-values as well. There is a command
in TI84 named 2: normalcdf() to find normal probabilities.
How to call the function 2: normalcdf()?
Follow the path below to call the command.
2ND+VARS >>> DISTR
>>>
When you scroll down under DISRT you will find the command, 2: normalcdf(). Use the command 2: normalcdf() to
find the left-tailed probability below X=x.
In this command, you need to plug the values of probability p, upper, µ, and
σ. Then after hitting the ENTER button twice you will get the desired normal
probability. The function provides options for both lower and upper values.
Therefore, unlike the excel function, the TI84 command gives both left-tailed and
right-tailed probabilities.
Illustration
Suppose X be a normal random variable with a mean of 10 and a standard deviation of 5. Find P(X < 17.8), P(X > 17.8).
In the command 2:
normalcdf() you need plug lower=-1E99, upper=17.8, µ=10 and σ=5.
Then hit the ENTER button twice, you will get P(X < 17.8) = 0.9406200496.
Use of TI84 calculator to find critical values
While constructing confidence intervals, we need to find critical values. These critical values are Z scores
corresponding to the given probability. There is a command in the TI84 calculator named 3: invNorm() to find normal
probabilities.
How to call the function 3: invNorm()?
Follow the path below to call the command.
2ND+VARS >>> DISTR
>>>
When you scroll down under DISRT you will find the command, 3: invNorm(). Use the command 3: invNorm() to find the critical value.
In this function, you need to plug the values of the left-tailed area, mean µ, and standard deviation σ. Then after hitting the ENTER button twice you will
get the desired critical value.
Illustration
Suppose you need to construct a 90% confidence interval for the population mean.
Assume that you know the value of population standard deviation in prior. What is
the critical value Z(α/2)?
The confidence
level for 90% confidence interval is, 0.90. This gives, significance level (α)
= 1-C = 1-0.90 = 0.10. The left tailed probability to the desired critical
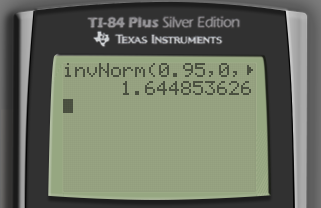
value Z(α/2) is, 1-(α/2) = 1-(0.10/2) = 1-0.05 = 0.95. Then in the command 3:
invNorm() you need to plug area=0.95, mean µ=0 and standard deviation σ=1.
Then hit the ENTER button twice, you will get the critical value Z(α/2) equals, 1.644853626.







2 Comments
Very good
ReplyDelete👌👌👌
ReplyDeletePost a Comment